Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen
O también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector. Módulo
Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo. Dirección
Viene dada por la orientación en el espacio de la recta que lo contiene. Sentido
Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Hay que tener muy en cuenta el sistema de referencia de los vectores, que estará formado por un origen y tres ejes perpendiculares. Este sistema de referencia permite fijar la posición de un punto cualquiera con exactitud.
El sistema de referencia que usaremos, como norma general, es el Sistema de Coordenadas Cartesianas.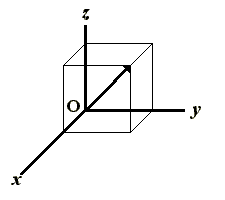 
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores unitarios. Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y corresponderán a cada uno de los ejes del sistema de referencia.
Por ello, al eje de las X, le dejaremos corresponder el vector unitario o también denominado .
Del mismo modo, al eje Y, le corresponderá el vector unitario o también denominado .
Finalmente, al eje Z, le dejaremos corresponder el vector unitario o también denominado .
Por tanto, obtendríamos un eje de coordenadas cartesianas de la siguiente forma:
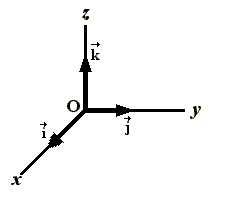
Una imagen vectorial es una imagen digital formada por objetos geométricos independientes (segmentos, polígonos, arcos, etc.), cada uno de ellos definido por distintos atributos matemáticos de forma, de posición, de color, etc. Por ejemplo un círculo de color rojo quedaría definido por la posición de su centro, su radio, el grosor de línea y su color.
Este formato de imagen es completamente distinto al formato de los gráficos rasterizados, también llamados imágenes matriciales, que están formados por píxeles. El interés principal de los gráficos vectoriales es poder ampliar el tamaño de una imagen a voluntad sin sufrir el efecto de escalado que sufren los gráficos rasterizados. Asimismo, permiten mover, estirar y retorcer imágenes de manera relativamente sencilla. Su uso también está muy extendido en la generación de imágenes en tres dimensiones tanto dinámicas como estáticas.
Todos los ordenadores actuales traducen los gráficos vectoriales a gráficos rasterizados para poder representarlos en pantalla al estar ésta constituida físicamente por píxeles.
Vector
Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que cabe distinguir: - Un origen o punto de aplicación: A.
- Un extremo: B.
- Una dirección: la de la recta que lo contiene.
- Un sentido: indicado por la punta de flecha en B.
- Un módulo, indicativo de la longitud del segmento AB.
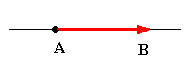
Gráfico vectorial
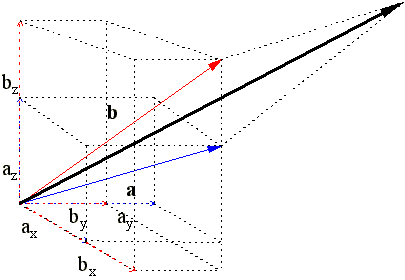
Módulo
Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo. Dirección
Viene dada por la orientación en el espacio de la recta que lo contiene. Sentido
Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Hay que tener muy en cuenta el sistema de referencia de los vectores, que estará formado por un origen y tres ejes perpendiculares. Este sistema de referencia permite fijar la posición de un punto cualquiera con exactitud.
El sistema de referencia que usaremos, como norma general, es el Sistema de Coordenadas Cartesianas.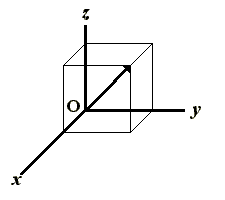
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores unitarios. Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y corresponderán a cada uno de los ejes del sistema de referencia.
Por ello, al eje de las X, le dejaremos corresponder el vector unitario o también denominado .
Del mismo modo, al eje Y, le corresponderá el vector unitario o también denominado .
Finalmente, al eje Z, le dejaremos corresponder el vector unitario o también denominado .
Por tanto, obtendríamos un eje de coordenadas cartesianas de la siguiente forma:
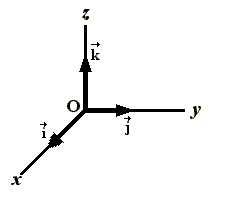
Una imagen vectorial es una imagen digital formada por objetos geométricos independientes (segmentos, polígonos, arcos, etc.), cada uno de ellos definido por distintos atributos matemáticos de forma, de posición, de color, etc. Por ejemplo un círculo de color rojo quedaría definido por la posición de su centro, su radio, el grosor de línea y su color.
Este formato de imagen es completamente distinto al formato de los gráficos rasterizados, también llamados imágenes matriciales, que están formados por píxeles. El interés principal de los gráficos vectoriales es poder ampliar el tamaño de una imagen a voluntad sin sufrir el efecto de escalado que sufren los gráficos rasterizados. Asimismo, permiten mover, estirar y retorcer imágenes de manera relativamente sencilla. Su uso también está muy extendido en la generación de imágenes en tres dimensiones tanto dinámicas como estáticas.
Todos los ordenadores actuales traducen los gráficos vectoriales a gráficos rasterizados para poder representarlos en pantalla al estar ésta constituida físicamente por píxeles.
Vector
Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que cabe distinguir: - Un origen o punto de aplicación: A.
- Un extremo: B.
- Una dirección: la de la recta que lo contiene.
- Un sentido: indicado por la punta de flecha en B.
- Un módulo, indicativo de la longitud del segmento AB.
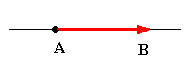
Gráfico vectorial
Sentido
Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Hay que tener muy en cuenta el sistema de referencia de los vectores, que estará formado por un origen y tres ejes perpendiculares. Este sistema de referencia permite fijar la posición de un punto cualquiera con exactitud.
El sistema de referencia que usaremos, como norma general, es el Sistema de Coordenadas Cartesianas.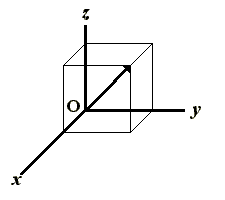
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores unitarios. Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y corresponderán a cada uno de los ejes del sistema de referencia.
Por ello, al eje de las X, le dejaremos corresponder el vector unitario o también denominado .
Del mismo modo, al eje Y, le corresponderá el vector unitario o también denominado .
Finalmente, al eje Z, le dejaremos corresponder el vector unitario o también denominado .
Por tanto, obtendríamos un eje de coordenadas cartesianas de la siguiente forma:
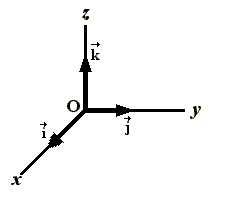
Una imagen vectorial es una imagen digital formada por objetos geométricos independientes (segmentos, polígonos, arcos, etc.), cada uno de ellos definido por distintos atributos matemáticos de forma, de posición, de color, etc. Por ejemplo un círculo de color rojo quedaría definido por la posición de su centro, su radio, el grosor de línea y su color.
Este formato de imagen es completamente distinto al formato de los gráficos rasterizados, también llamados imágenes matriciales, que están formados por píxeles. El interés principal de los gráficos vectoriales es poder ampliar el tamaño de una imagen a voluntad sin sufrir el efecto de escalado que sufren los gráficos rasterizados. Asimismo, permiten mover, estirar y retorcer imágenes de manera relativamente sencilla. Su uso también está muy extendido en la generación de imágenes en tres dimensiones tanto dinámicas como estáticas.
Todos los ordenadores actuales traducen los gráficos vectoriales a gráficos rasterizados para poder representarlos en pantalla al estar ésta constituida físicamente por píxeles.
Vector
Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que cabe distinguir: - Un origen o punto de aplicación: A.
- Un extremo: B.
- Una dirección: la de la recta que lo contiene.
- Un sentido: indicado por la punta de flecha en B.
- Un módulo, indicativo de la longitud del segmento AB.
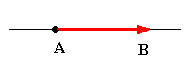
Gráfico vectorial
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores unitarios. Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre sí y corresponderán a cada uno de los ejes del sistema de referencia.
Del mismo modo, al eje Y, le corresponderá el vector unitario o también denominado .
Finalmente, al eje Z, le dejaremos corresponder el vector unitario o también denominado .
Por tanto, obtendríamos un eje de coordenadas cartesianas de la siguiente forma:
Una imagen vectorial es una imagen digital formada por objetos geométricos independientes (segmentos, polígonos, arcos, etc.), cada uno de ellos definido por distintos atributos matemáticos de forma, de posición, de color, etc. Por ejemplo un círculo de color rojo quedaría definido por la posición de su centro, su radio, el grosor de línea y su color.
Este formato de imagen es completamente distinto al formato de los gráficos rasterizados, también llamados imágenes matriciales, que están formados por píxeles. El interés principal de los gráficos vectoriales es poder ampliar el tamaño de una imagen a voluntad sin sufrir el efecto de escalado que sufren los gráficos rasterizados. Asimismo, permiten mover, estirar y retorcer imágenes de manera relativamente sencilla. Su uso también está muy extendido en la generación de imágenes en tres dimensiones tanto dinámicas como estáticas.
Todos los ordenadores actuales traducen los gráficos vectoriales a gráficos rasterizados para poder representarlos en pantalla al estar ésta constituida físicamente por píxeles.
Vector
Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que cabe distinguir:- Un origen o punto de aplicación: A.
- Un extremo: B.
- Una dirección: la de la recta que lo contiene.
- Un sentido: indicado por la punta de flecha en B.
- Un módulo, indicativo de la longitud del segmento AB.
Gráfico vectorial
El número de oro en el arte, el diseño y la naturaleza
El número áureo aparece, en las proporciones que guardan edificios, esculturas, objetos, partes de nuestro cuerpo, ...
Un ejemplo de rectángulo áureo en el arte es el alzado del Partenón griego.
En la figura se puede comprobar que AB/CD=
. Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD= y CD/CA=.
. Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD= y CD/CA=.
Hay un precedente a la cultura griega donde también apareció el número de oro. En La Gran Pirámide de Keops, el cociente entre la altura de uno de los tres triángulos que forman la pirámide y el lado es 2.
Ya vimos que el cociente entre la diagonal de un pentágono regular y el lado de dicho pentágono es el número áureo. En un pentágono regular está basada la construcción de la Tumba Rupestre de Mira en Asia Menor. 
Ejemplos de rectángulos áureos los podemos encontrar en las tarjetas de crédito, en nuestro carnet de identidad y también en las cajetillas de tabaco.Unas proporciones armoniosas para el cuerpo, que estudiaron antes los griegos y romanos, las plasmó en este dibujo Leonardo da Vinci. Sirvió para ilustrar el libro La Divina Proporción de Luca Pacioli editado en 1509. 
En dicho libro se describen cuales han de ser las proporciones de las construcciones artísticas. En particular, Pacioli propone un hombre perfecto en el que las relaciones entre las distintas partes de su cuerpo sean proporciones áureas. Estirando manos y pies y haciendo centro en el ombligo se dibuja la circunferencia. El cuadrado tiene por lado la altura del cuerpo que coincide, en un cuerpo armonioso, con la longitud entre los extremos de los dedos de ambas manos cuando los brazos están extendidos y formando un ángulo de 90º con el tronco. Resulta que el cociente entre la altura del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano (radio de la circunferencia) es el número áureo.
El cuadro de Dalí Leda atómica, pintado en 1949, sintetiza siglos de tradición matemática y simbólica, especialmente pitagórica. Se trata de una filigrana basada en la proporción áurea, pero elaborada de tal forma que no es evidente para el espectador. En el boceto de 1947 se advierte la meticulosidad del análisis geométrico realizado por Dalí basado en el pentagrama místico pitagórico.
En la naturaleza, aparece la proporción áurea también en el crecimiento de las plantas, las piñas, la distribución de las hojas en un tallo, dimensiones de insectos y pájaros y la formación de caracolas.La espiral logarítmica
Si tomamos un rectángulo áureo ABCD y le sustraemos el cuadrado AEFD cuyo lado es el lado menor AD del rectángulo, resulta que el rectángulo EBCF es áureo. Si después a éste le quitamos el cuadrado EBGH, el rectángulo resultante HGCF también es áureo. Este proceso se puede reproducir indefinidamente, obteniéndose una sucesión de rectángulos áureos encajados que convergen hacia el vértice O de una espiral logarítmica.
Esta curva ha cautivado, por su belleza y propiedades, la atención de matemáticos, artistas y naturalistas. Se le llama también espiral equiangular (el ángulo de corte del radio vector con la curva es constante) o espiral geométrica (el radio vector crece en progresión geométrica mientras el ángulo polar decrece en progresión aritmética). J. Bernoulli, fascinado por sus encantos, la llamó spira mirabilis, rogando que fuera grabada en su tumba.
La espiral logarítmica vinculada a los rectángulos áureos gobierna el crecimiento armónico de muchas formas vegetales (flores y frutos) y animales (conchas de moluscos), aquellas en las que la forma se mantiene invariante. El ejemplo más visualmente representativo es la concha del nautilus.
La trigonometría y el número de oro
Consideremos un pentágono regular en el cual se han dibujado las diagonales. 
En esta figura sólo aparecen tres ángulos diferentes. Miden 36º, 72º y 108º. La relación entre estos ángulos es la siguiente: 72 es el doble de 36 y 108 es el triple de 36. Hay varios tipos diferentes de triángulos isósceles, de los cuales seleccionamos tres: los triángulos ABE, ABF y AFG. El resto de triángulos son semejantes a alguno de estos y no aportan información adicional. Finalmente, hay cuatro segmentos diferentes en estos triángulos, que llamaremos: BE=a, AB=AE=b, AF=BF=AG=c y GF=d. Las longitudes de estos segmentos cumplen: a>b>c>d.
En esta figura sólo aparecen tres ángulos diferentes. Miden 36º, 72º y 108º. La relación entre estos ángulos es la siguiente: 72 es el doble de 36 y 108 es el triple de 36. Hay varios tipos diferentes de triángulos isósceles, de los cuales seleccionamos tres: los triángulos ABE, ABF y AFG. El resto de triángulos son semejantes a alguno de estos y no aportan información adicional. Finalmente, hay cuatro segmentos diferentes en estos triángulos, que llamaremos: BE=a, AB=AE=b, AF=BF=AG=c y GF=d. Las longitudes de estos segmentos cumplen: a>b>c>d.Consideremos cada uno de estos triángulos por separado y apliquemos el teorema del seno.
Triángulo ABE
Triángulo ABF
Triángulo AFG
Como 72º=180º-108º, se verifica que sen72º=sen108º.
En consecuencia podemos establecer las siguientes proporciones:
Es decir, una vez ordenadas las longitudes de los cuatro segmentos de mayor a menor, la razón entre cada una de ellas y la siguiente es constante e igual a nuestro número de oro.
Tomando la primera de las proporciones, teniendo en cuenta que c=a-b y haciendo b=1:
(el numero de oro)Es decir, dos de estos segmentos consecutivos cumplen la proporción áurea.
Como consecuencia, se verifica 
.
.
Curiosidades áureas
Potencias. Los números 
guardan unas curiosas relaciones entre si. Efectivamente, podemos deducirlas a partir de la ecuación 
que tiene como solución el número de oro:
guardan unas curiosas relaciones entre si. Efectivamente, podemos deducirlas a partir de la ecuación que tiene como solución el número de oro: 
Potencias 2. Consideremos la sucesión de término general: 
. Si calculamos los primeros términos, podemos observar una curiosa relación entre ellos. Calculando primero algunas potencias
. Si calculamos los primeros términos, podemos observar una curiosa relación entre ellos. Calculando primero algunas potencias
podemos concluir que la sucesión dada se convierte en
Evidentemente, cada término a partir del tercero se puede obtener sumando los dos anteriores. Lo curioso es que esta relación es la misma que se verifica en la sucesión de Fibonacci.
Limites. Comprobemos que los siguientes límites dan como resultado el número de oro:
1 2
1 2
1. Llamemos "L" al valor del límite. Fácilmente se comprueba que se verifica la ecuación 
. Elevando al cuadrado los dos miembros y pasando todos los términos a la izquierda se obtiene la ecuación final 
. Una de las soluciones de esta ecuación es nuestro número de oro 
.
. Elevando al cuadrado los dos miembros y pasando todos los términos a la izquierda se obtiene la ecuación final . Una de las soluciones de esta ecuación es nuestro número de oro .2. Sea "M" el valor del límite. Se comprueba la relación 
. Quitando denominadores y pasando todos los términos a la izquierda se obtiene la ecuación 
cuya solución positiva es el número de oro.
. Quitando denominadores y pasando todos los términos a la izquierda se obtiene la ecuación cuya solución positiva es el número de oro.
Referencias
http://www.slideshare.net/jose.roblesbatista/magnitudes-escalares-y-vectoriales-presentation-590863
http://www.tochtli.fisica.uson.mx/electro/vectores/definici%C3%B3n_de_vectores.htm
No hay comentarios:
Publicar un comentario